Abstract: We develop a method for clustering English verbs into classes based on their occurrence with other words in a corpus. Our automatic clustering is an attempt to replicate the hand-clustering done by Beth Levin [11]. We generate a graph from the corpus with edges between words that appear together in some sentence. We then partition the graph using spectral partitioning. This method of partitioning verbs does not seem to work well on such limited data. There are obvious gains had by processing sentences and sending data to Matlab in parallel, but due to the current poor implementation of sparse matrices in the STAR*P language, it is not currently faster to do spectral partitioning in parallel.
The goal of our project is the automated parallel determination of Levin verb classes [11]. Levin verb classes capture the way in which different verbs are used with objects, prepositions, subjects, and other parts of a sentence. If two verbs can be used in the same way with the same words, they fall into the same class. From a linguistic perspective, identifying verb classes allows us to see connections between two or more verbs that do not exist between others in different classes.
To accomplish this classification automatically, we take a parsed corpus which has assigned part-of-speech tags to each of the words and a tree structure to the sentence. After extracting the relevant words from the trees, we then transform words with selected parts of speech from the corpus into a graph and partition it using the spectral partitioning algorithm. We compute the eigenvectors of the Laplacian matrix of the graph and use these vectors to split the graph into clusters. We may then analyze the effectiveness of our clustering by comparing our classifications against those done by hand by Levin (listed here).
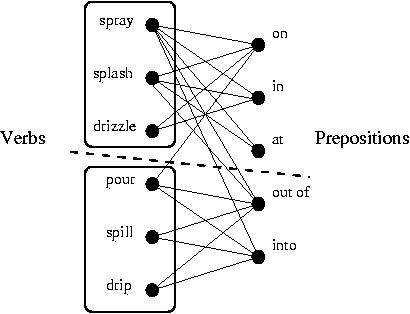
For example, the following image shows a partitioning of a small set of verbs into classes based on a bipartite graph of their co-occurrence with prepositions in the corpus. In this case, for instance, we observed the verb "pour" in a sentence with the preposition "on," but never with "at," so there is an edge between the former but not the latter. The dashed line indicates the partition, and the two boxes the verbs in each cluster.

We have implemented each part of our algorithm in parallel using the C MPI library and the sparse matrix packages of Matlab STAR*P.
The rest of this report is structured as follows. We first review existing work on automatic verb classification and parallel clustering algorithms. We then describe the three parts of our algorithm in more detail. Finally, we describe several of our results.
There has been a decent amount of work in the last decade or so on automatically acquiring lexical semantic information about verbs. This sort of information is useful not only as a sort of grammar dictionary of how verbs can be used, which is useful in many natural language processing tasks, but also many people believe that verbs with the same classification have very similar meanings. For example, if a full lexical semantic classification for verbs could be found, it might be possible to automatically learn the general meanings of verbs in a novel language.
Much of this research was inspired, as ours is, by Beth Levin's 1993 book, English Verb Classes and Alternations [11]. Levin classified many English verbs into 191 different categories based on their assignment of semantic arguments to different syntactic positions and their diathesis alternations, which involve how the same semantic argument can move to a different syntactic position. For example, I can say "broke the glass" or "the glass broke." Levin also showed that these classes are strongly correlated with the meaning of the verbs. Levin did all this work manually over 30 years, so there really is a use for automatic methods. Levin's work inspired a reasonable amount of related work attempting to derive verb classes in an easier and more automatic way.
Dorr and Jones [5] argue that syntactic classification frames can be used to organize verbs into their Levin classes. Syntactic frames account for the different arguments that a verb takes; for example, NP V NP PP(in) or NP V NP is an syntactic frame. They believe that verbs can be classified according to the syntactic frames that they allow and disallow. 98% of Levin classes differ in their syntactic frames, so Dorr and Jones argue that if one can differentiate the same verbs with different meanings and correctly identify syntactic frames, one can also find Levin classes with 98% correctness.
Schulte im Walde is one person who is currently working on automatic statistical techniques for classifying English and German verbs based on their syntactic frames into Levin classes for English and automatic clustering for German. Her results show that the technique has promise, in that it is much better than guessing, but there is still clearly work to be done [7]. Im Walde also experiments with different algorithms for clustering including the standard k-Means.
McCarthy has worked on the automatic acquisition of diathesis alternations using the WordNet database [12]. Using WordNet, McCarthy correctly identified whether or not a verb had a given alternation with 70% accuracy. Without WordNet, the accuracy dropped to 60%. Again, this is above the guessing average of 50%, but the technique is far from perfected.
There are various other people producing papers researching automatic verb clasification and related lexical semantics. Gildea and Jurafsky [6] attempted to infer the syntactic frame and semantic role assignment for verbs by examining their probabilities on manually annotated training data. Lapata and Brew [10] use statistical frequencies of verbs and verb classes along with syntactic frames to try to automatically classify a specific usage of a verb into its Levin class. Brisco and Carroll [2] also attempt to automatically identify what the syntactic frame of a verb is. Merlo and Stevenson [14] use five features of verb usage to classify the verbs into 3 different categories, based on transitivity. The is particularly interesting because the 3 categories occur in the same syntactic frame. Merlo, Stevenson, Tseng, and Allaria [13] build on this framework but attempt to lower the error by doing multilingual comparisons to translated verbs. Joanis [9] wrote his thesis on using a general feature space instead of specific features, which performed with about the same accuracy, though picking features at random lead to a great deal more error.
There is a decent amount of work in this new area regarding different possible methods of classifying verbs automatically. As far as we can tell, there has been no work on parallelizing any of these methods. Because most of the methods rely on already annotated text, relatively small training corpuses, and already created databases such as FrameNet and WordNet, there is less of a need for speed than if the methods attempted to use the data of a full web crawl, for example. So there is still a great deal of useful work to be done in writing code that classifies verbs correctly and quickly.
Many algorithms exist for clustering nodes in bipartite graphs. Dhillon's algorithm [4] performs co-clustering, simultaneously clustering both documents and words by using the technique of spectral graph partitioning. This solution is equivalent to finding minimum cut vertex partitions on the graph. As this problem is NP-complete, a relaxation of it is solved using the second left and right singular vectors of the matrix representing the graph. Other relevant bipartite clustering algorithms are those of Zha et. al. [15] and Chen et. al. [3].
Our clustering implementation is based on code from the
Meshpart
toolkit, a collection of methods for graph and mesh partitioning.
In particular, the specpart method implements spectral
partitioning, although it has two limitations when considering a
parallel implementaiton. First, utilizes the Cholesky decomposition
of the Laplacian matrix to find the Fiedler (second) eigenvector.
This decomposition is slow in parallel, so we have chosen to use a
different, iterative method for finding eigenvectors. In addition,
the existing specpart implementation only partitions the
graph into two parts. We extend this scheme in several ways to
partition our graph into many clusters, as this is especially
important for our task of verb classification.
Due to both time constraints and the high quality of the corpus, preparsed data from the Wall Street Journal corpus was used. This data is valuable because the parses are quite accurate and the corpus sentences are not ungrammatical, so it avoids many of the problems of bad data associated with using a parser that is not tuned to your data set. It also avoids issues that arise from using text scraped from the World Wide Web, or spoken corpus data which are often ungrammatical. Tokenizers, which divide the words up into their morphemes, were also abandoned because of the great deal of processing time they took in exchange for possibly making the data worse. For example, the PC Kimmo tokenizer would split the verb realize into re+al+ize, giving 'al' as the main verb.
This data was processed in an embarassingly parallel fashion by having a C MPI program which called a perl script which extracted the tree structure from the corpus, extracted the relevant words from the sentences, then output the words to file as tab separated values for easier processing by Matlab.
A sparse matrix A is constructed in Matlab using three vectors, i, j, and s. The i and j vectors specify indices into the new sparse matrix, and the s vector specifies the values at the respective indices. That is, if i[0] = 25, j[0] = 13, and s[0] = 2, then A[25, 13] = 2. In STAR*P, the construction is similar, but i, j, and s may be distributed vectors.
To create the incidence matrix required for spectral partitioning, we need to ensure that each process uses the same indexing scheme for the words it has encountered in the corpus. For instance, if both processes 3 and 4 encounter the word "spray" during their parsing, they must both assign the same index i to "spray" for the purpose of constructing the sparse matrix A. If they do not, A will not correctly represent the incidence graph. Thus we are faced with the problem of creating a consistent indexing scheme for the words in the corpus across processors.
One easy way to create this index would be to bring the "vocabulary list" from each process to the front end, merge them, index the full list, and then redistribute the full index back to the processes. This scheme is shown in the image below:
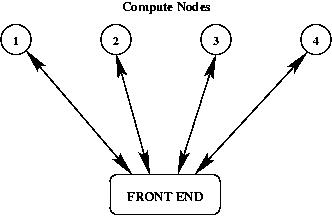
However, if we plan to partition our graph in parallel, as described in the next section, it is counterproductive in terms of communication time to bring the entire list to the front end - if this were the case we might as well utilize the serial version of spectral partitioning.
Instead, we adopt a scheme to index the distributed vocabulary lists without bringing them to the front end. We begin by passing the outermost processes' (1 and 4) lists to their neighbors (2 and 3). These neighbors then merge these with their own lists, changing indices as necessary. Nodes 2 and 3 then swap lists and reindex. Finally, nodes 2 and 3 pass their lists back to nodes 1 and 4. Each node now has a full vocabulary list with indices consistent with the other processes, and we can construct the parallel sparse matrix correctly. A schematic of this process is shown below:
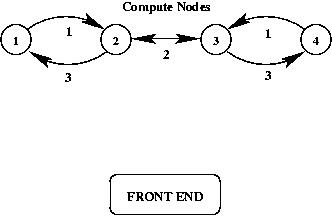
This scheme is an improvement in two ways. First, it saves on the total number of inter-process communications required. As shown in the images above, we require 6 communications versus the 8 for the front-end scheme. Second, the size of these communications is reduced. The only communications that are sending the full vocabulary list are those labeled "3" in the diagram above. In contrast, the front-end scheme has four communications of the full list, one to each compute node.
As mentioned above, we have chosen spectral partitioning as our partitioning algorithm. This choice was motivated by the fact that our graphs are highly non-planar, which makes mesh-type partitioning techniques such as geometric partitioning ineffective. Spectral partitioning, on the other hand, relies on the underlying mathematical structure of the graph, which makes it more suited for graphs with no physicality, such as the semantic structure of English words.
The standard version of the spectral algorithm finds partitions using the second (Fiedler) eigenvector of the Laplacian matrix of the graph. (We ignore the first eigenvector, as its eigenvalue is always zero for a conncted graph.) Once this eigenvector is found, the nodes of the graph are partitioned by splitting the values of the eigenvector around its median value.
The original specpart routine from the Meshpart
toolkit had two drawbacks for our problem. First, it made use of the
Cholesky decomposition to find the eigenvectors of the Laplacian
matrix of the graph. This decomposition is not only "overkill" for
our problem, as we only need a few eigenvectors, but it is slower than
alternative, iterative methods. Instead, we chose to utilize Matlab's
eigs method to find eigenvectors. This approach has two
benefits: first, it allows us to only calculate as many eigenvectors
as we need for partitioning, rather than all of them, and second, it
is more easily parallelizable than the alternatives.
The second drawback to the original code is that it only partitions the graph into two parts. For our classification problem, we would like to cluster verbs into many more groups. To resolve this, we utilize other eigenvectors of the Laplacian. For instance, to partition into four groups, we find the second and third eigenvectors. We split the graph twice, first around the median of the second eigenvector. We then re-split each cluster around the median of the third eigenvector. In this way we can cluster the nodes into 2n groups.
The iterative nature of eigs allows spectral
partitioning to be more easily parallelized. In STAR*P we simply make
the input graph A and its Laplacian L sparse, distributed matrices.
Within eigs, we simply parallelize the matrix C = L -
σ * I and the random vector y. σ is a "guess" at the
value of the eigenvalue, and eigs will converge on the
closest eigenvalue to σ.
To find the first n eigenvectors, skipping the zero eigenvalue, we
initialize σ to 0.0025. We then iterate, calling
eigs on each loop and checking the value returned to see
if it is not 0. If it is still 0, we double our σ guess, and
continue. When we find a non-zero eigenvalue, we store its
eigenvector. We then increment σ and continue, looking for the
next eigenvector by successively doubling σ. We continue this
way until we have found as many eigenvectors as we require for
partitioning.
Once the required eigenvectors have been found, partitioning is easy. The partition number, ρi, of a node i is simply:
We have three main results: the ability to reindex the vocabulary
lists on separate processors faster than bringing them to the front
end, the speed of parallelizing the spectral partitioning algorithm
using eigs and Matlab STAR*P's sparse matrix support, and
the effectiveness of our clustering when compared to Levin's
hand-classified verbs.
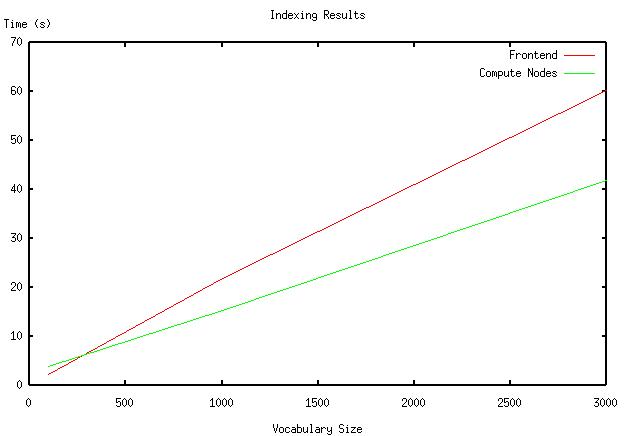
Our reindexing algorithm proved to be fairly effective in sharing an indexing scheme between the processors faster than bringing all data to the front end. The following graph gives the time taken for the naive frontend scheme to index the full list versus our parallel indexing scheme for various vocabulary sizes. We note that for small vocabularies, the front-end processing is faster, as it requires fewer steps. As we increase the vocabulary size, however, the amount of data being transferred in each step means that our parallel scheme is faster.
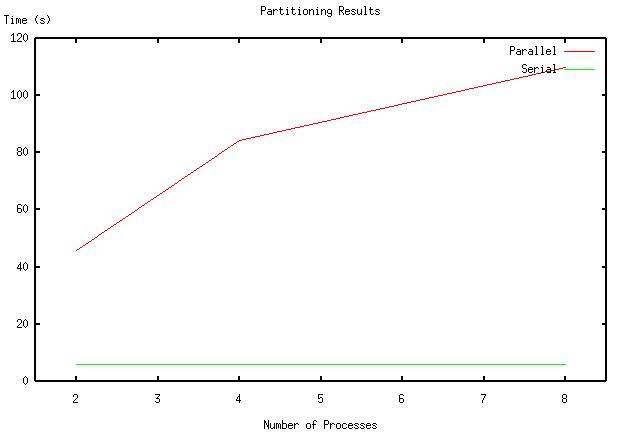
In theory, our parallel implementation of spectral partitioning
should see speed increases due to sharing the iterative calculation of
eigenvectors in eigs among several processors. In
practice, unfortunately, this was not the case. It appears that the
sparse matrix implementation in STAR*P has a large amount of
communication overhead for constructing and indexing sparse matrices
across processors. This overhead, in practice, as shown in the graph
below, significantly slowed down our parallel version when compared to
the serial partitioning algorithm.
The following graph gives the time taken by our serial version of
specpart (using serial eigs) versus the time
taken by our parallel specpart:
Finally, a graph comparing clusters derived from our algorithm against random clustering is shown below. We generated these percentages by choosing verbs pairwise from each cluster and checking them against the Levin classes to determine if they actually appeared in the same class. Random data was generated by randomly assigning each verb a class and then doing the same pairwise count.
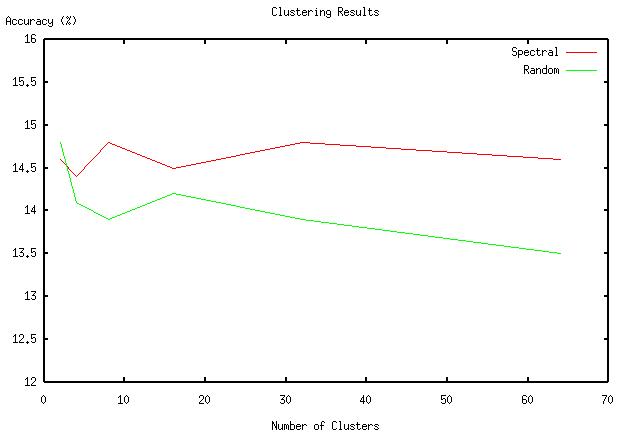
We note that for a small number of clusters (2) our algorithm does about the same as random, most likely because with only two clusters there is not much real classification going on. As we increase the number of clusters, our partitioning algorithm does beat random, but not by a statistically significant amount.
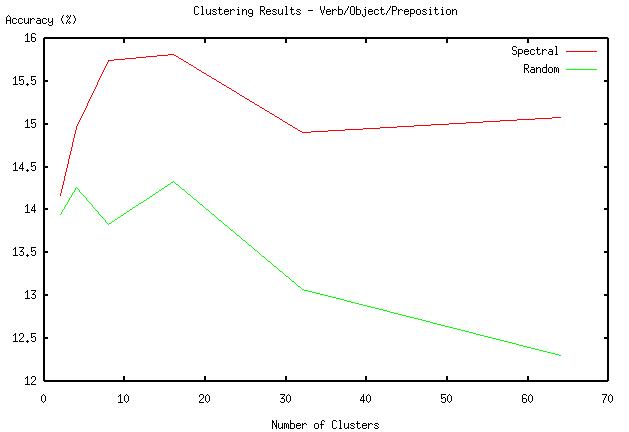
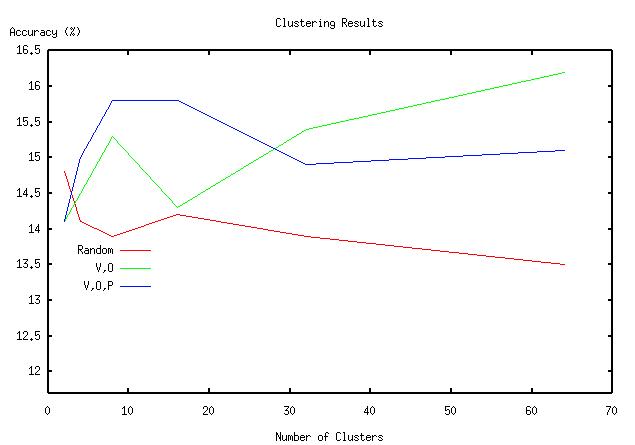
After closer analysis, we decided that these results might be poor because we built our graph from five parts of speech in the parsed sentences: subject, verb, object, preposition, and prepositional object. We hypothesized that taking fewer columns might reduce the amount of noise in the graph and give us better clusters. The results for the {verb,object,preposition} set are given below, and show a significant improvement in accuracy over the full dataset.
The results for many of the possible combinations of {subject, object, preposition, object of preposition} are given below.
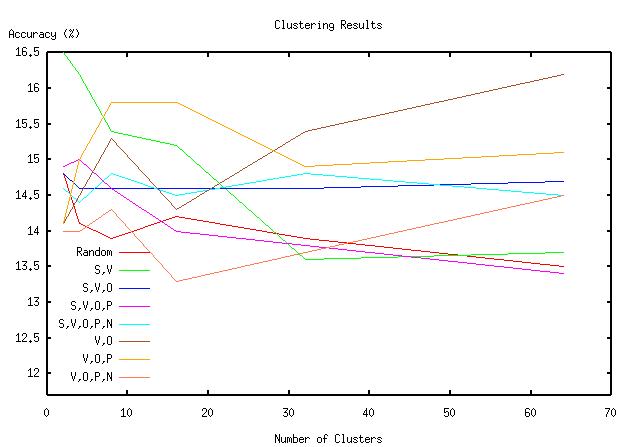
These are the best results of those many combinations. It is experimentally interesting though not overly surprising that the best results come from the subcatagorized object and preposition as opposed to the subject or object of the preposition.
One other aspect might explain our poor clustering results. Our data was generated from a very restricted corpus of financial articles from the Wall Stree Journal. By expanding our corpus to include more varied verbs, we would expect to see better clustering results.
Since our results were not as good as we would hoped, for future work we would want to use a great deal more data. In the current implementation, due to the relative difficulty of getting tagged input to a parser in the form necessary for the parser and then stripping out the necessary data from the parser, compared to the originally perceived benefit of having more data of lesser quality, we elected to only use preparsed data. We also elected not to use a tokenizer due to the mediocrity of available free tokenizers. Not using a tokenizer forced us to judge the correctness of the data by throwing out all verbs which were not in predetermined Levin classes, which is a great amount of the untokenized data. All these factors combined to give, overall, a relatively small amount of data to work with.
For future work, we would use a parser and possibly a tokenizer. Using a parser would give us access to a much greater variety of corupuses and a much greater amount of data. Having enough parsed data would lessen the need for a tokenizer, though if speed were not an issue, adding a tokenizer would be helpful as long as the Levin verb gold standard were also passed through the tokenizer so that the errors introduced in tokenizing would not unfairly hurt the results.
This method does not merely apply to verb clustering. It would be very interesting to use the same method to group nouns, for example. It seems likely that a given verb or preposition will subcatagorize for a specific class of noun. For example, for the most part only edible things are eaten by animate nouns. It would be difficult to evaluate such results, since there is no gold standard for noun clustering as there is for verb clustering. Nonetheless, if the method worked, it would be a great way for figuring out, for instance, what important features are and where such features are subcatagorized for. This data could be exptrapolated to give a machine learning approach to "common sense".
It would also be nice to see what the speedup would be on the spectral partitioning problem under a debugged version STAR*P sparse matrices. Even with our limited data, this method takes a noticible amount of time. With exponentially more data, the parallel aspect of the partitioning implementation would become increasingly necessary.
Even though our implementation was not as successful as we might have hoped, we believe that it still shows promise.
specpartspecparteigseigs